About Me

My name is CHEN Xiao (陳 嘯). I am currently pursuing a Ph.D. in Mathematics at Tsinghua University under the supervision of Prof. HUANG Yi (黃 意). My research interests include hyperbolic geometry, knot theory, combinatorial topology, and Teichmüller theory.
Beyond mathematics, I am also engaged in research on Chinese dialectology, with a particular focus on the Hangzhou dialect, a subvariety of Wu Chinese.
Email: x-chen20 AT mails DOT tsinghua DOT edu DOT cn
Talks
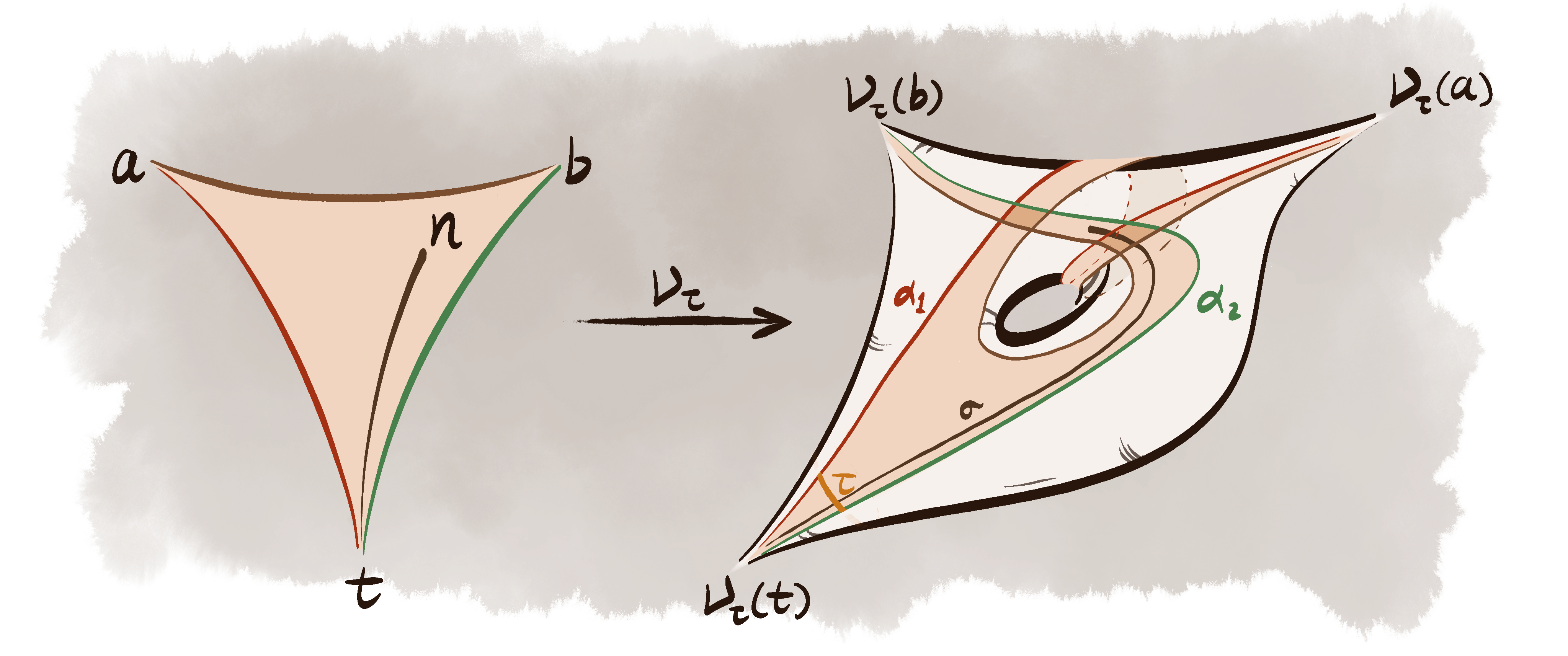
Geometric Intersection Complexes
January 2025Maximal Systems of Curves on Surfaces
October 2024Maximal Systems of Curves
September 2024Maximal Systems of Curves Intersecting Pairwise Once on Non-Orientable Surfaces
April 2024Maximal Systems of Intersecting Curves on Surfaces
December 2023Maximal Systems of Intersecting Curves on Surfaces
December 2023Seminars
G2T2 Seminar
Beijing
2025-
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Organizers:
Yifei CAI, Xiao CHEN, Diptaishik CHOUDHURY, Qiliang LUO, Tuo SUN, Ivan TELPUKHOVSKIY, and Daxun WANG
Latest Seminar:
Time: June 6, 2025, 10:00 AM
Place: Ningzhai 203
Speaker: Kyle FULLER (Rensselaer Polytechnic Institute)
Title: A Discussion of Goodstein's Theorem and the Kirby-Paris Hydra Theorem
Abstract:
We begin by introducing Goodstein's theorem and the Kirby-Paris hydra theorem, two well-known results that are expressible in the language of Peano Arithmetic but are beyond its ability to prove. We then review some relevant background from mathematical logic, including Gödel's incompleteness theorems, Gentzen's result on the consistency of Peano Arithmetic, and transfinite ordinals. Next, we cover a proof of both Goodstein's theorem and the Kirby-Paris hydra theorem. Finally, we discuss a surprising result by Kirby and Paris, who built on the foundational work of Gödel, Gentzen, and others to show that both theorems are unprovable in Peano Arithmetic.
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Latest Seminar:
YMSC Topology Seminar
The YMSC Topology Seminar is devoted to frontier topics in topology, geometry, and related fields. It regularly invites scholars from across the mathematical community to share their work and engage in meaningful exchange, with the aim of fostering academic dialogue and broadening intellectual horizons.