About Me

My name is CHEN Xiao (陳 嘯). I received my Ph.D. in Mathematics from Tsinghua University, under the supervision of Prof. HUANG Yi (黃 意). My research interests include hyperbolic geometry, knot theory, combinatorial topology, and Teichmüller theory. Here is my Curriculum Vitae.
Beyond mathematics, I am also engaged in research on Chinese dialectology, with a particular focus on the Hangzhou dialect, a subvariety of Wu Chinese.
Email: x-chen20 [AT] tsinghua [DOT] org [DOT] cn
Research & Publications
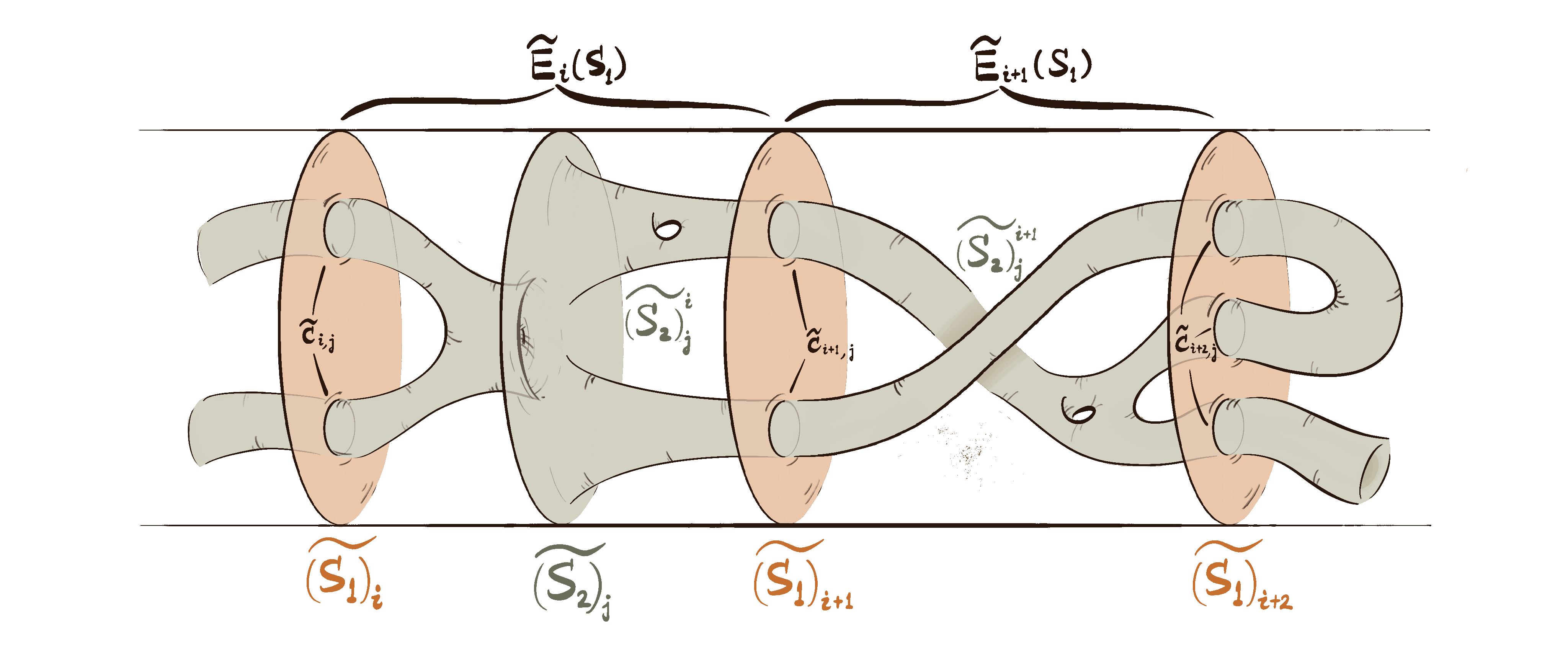
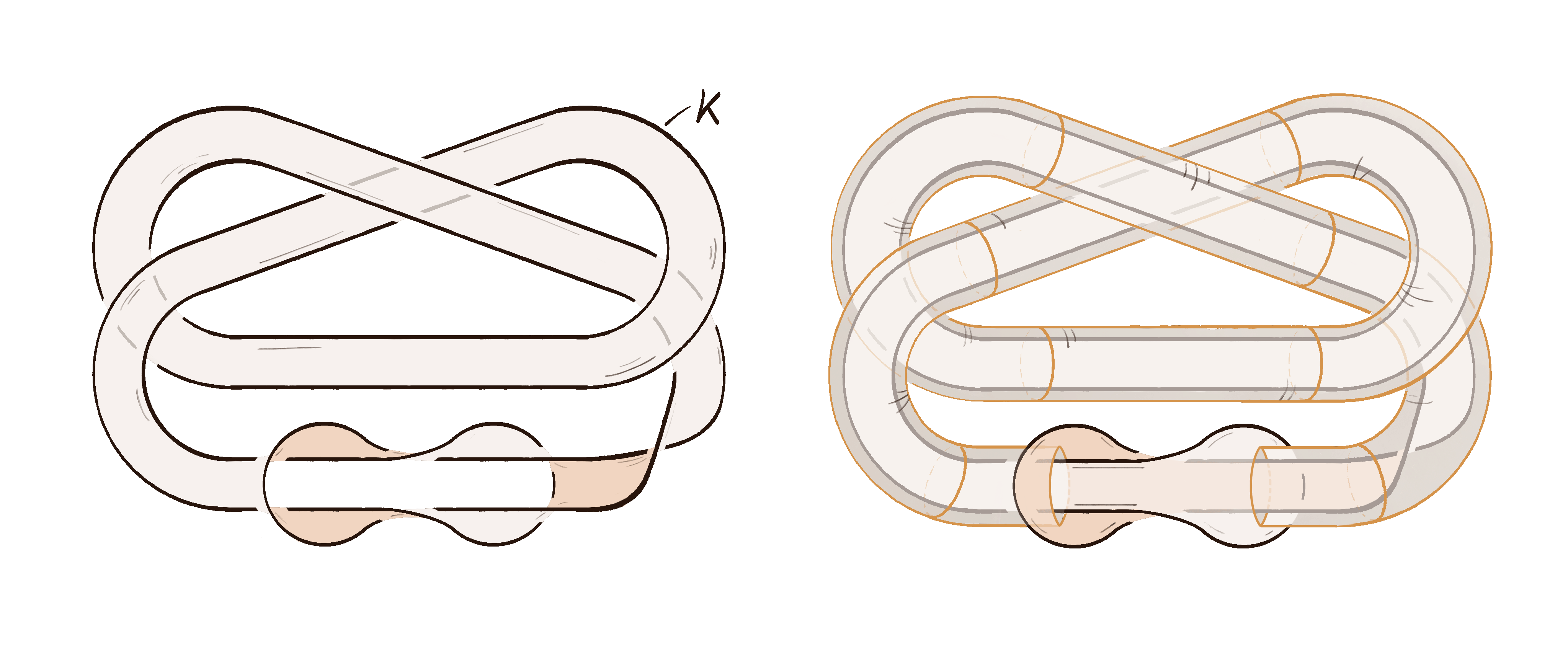
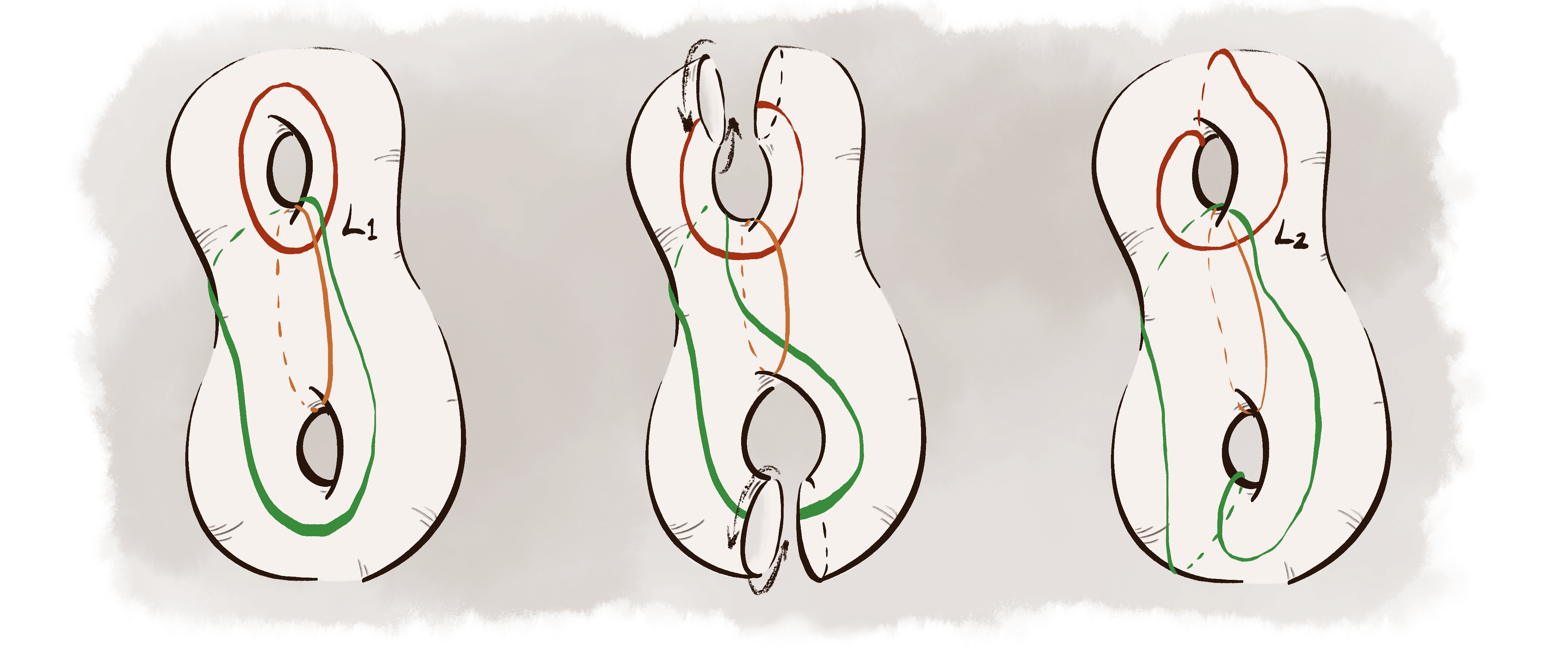
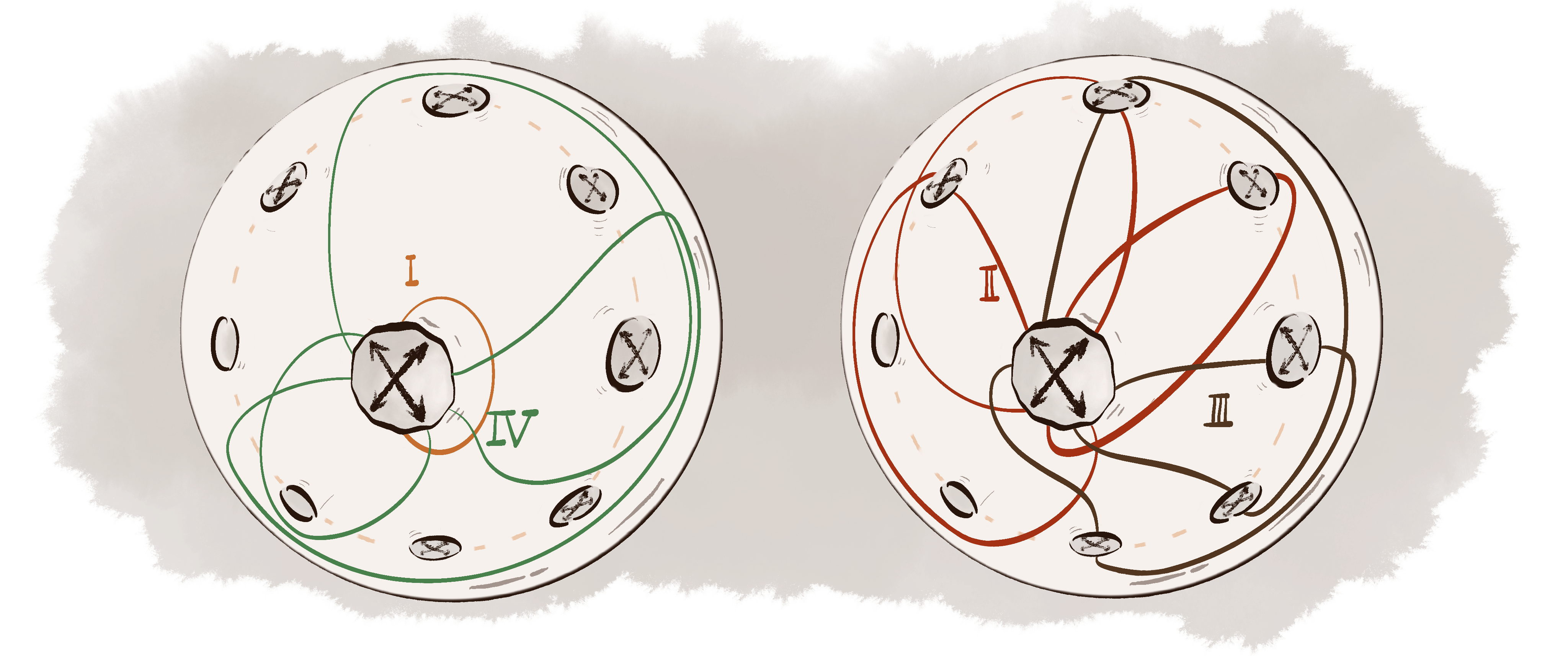
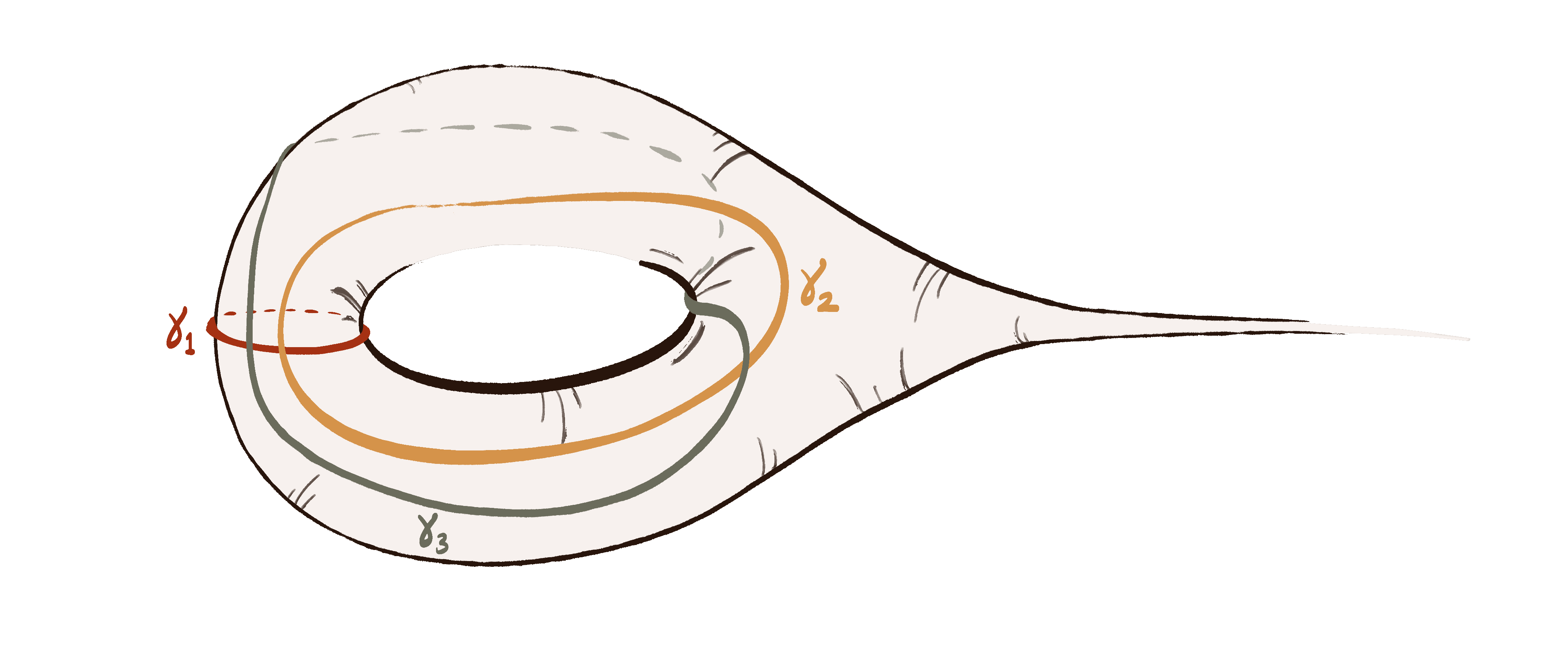
A Linear Bound on the Diameter of the Kakimizu Complex for Hyperbolic Knots (Joint with Wujie Shen)
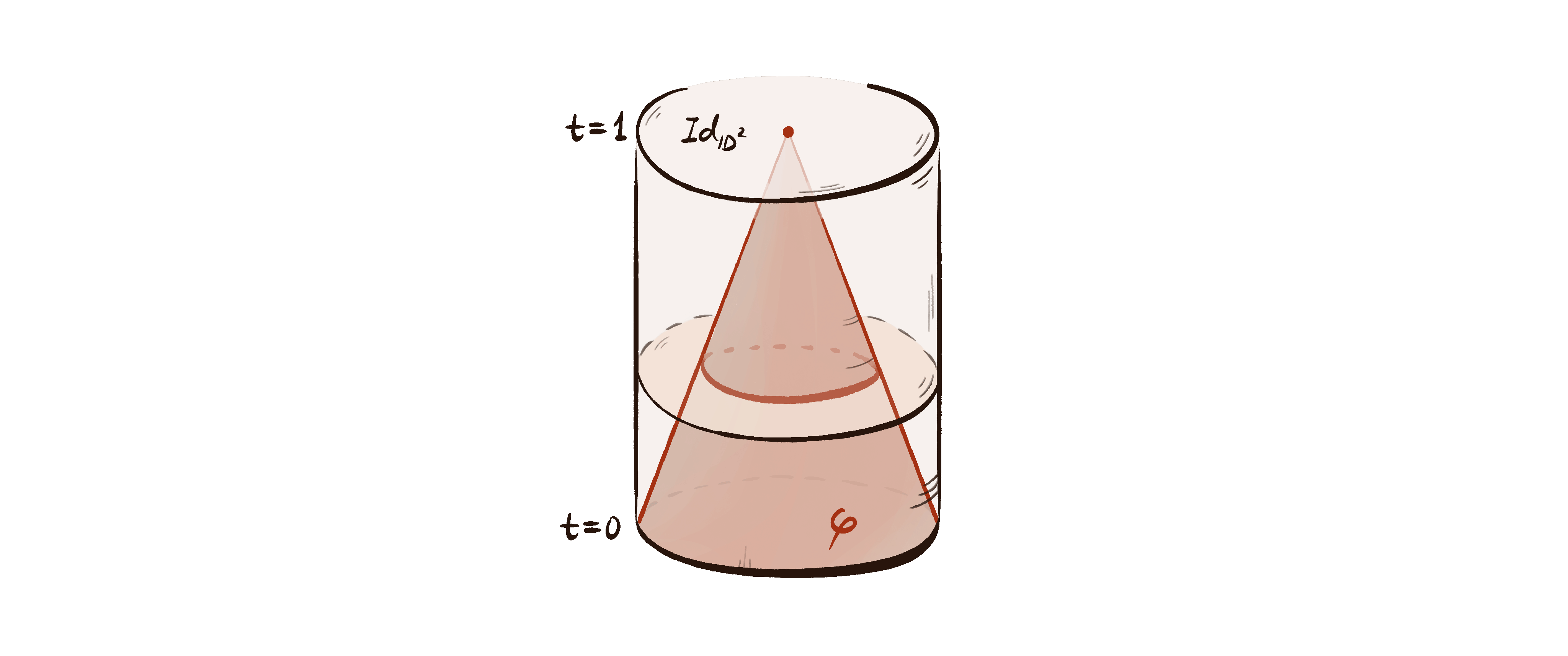
Uniqueness of Maximal Curve Systems on Punctured Projective Planes (Joint with Wujie Shen)
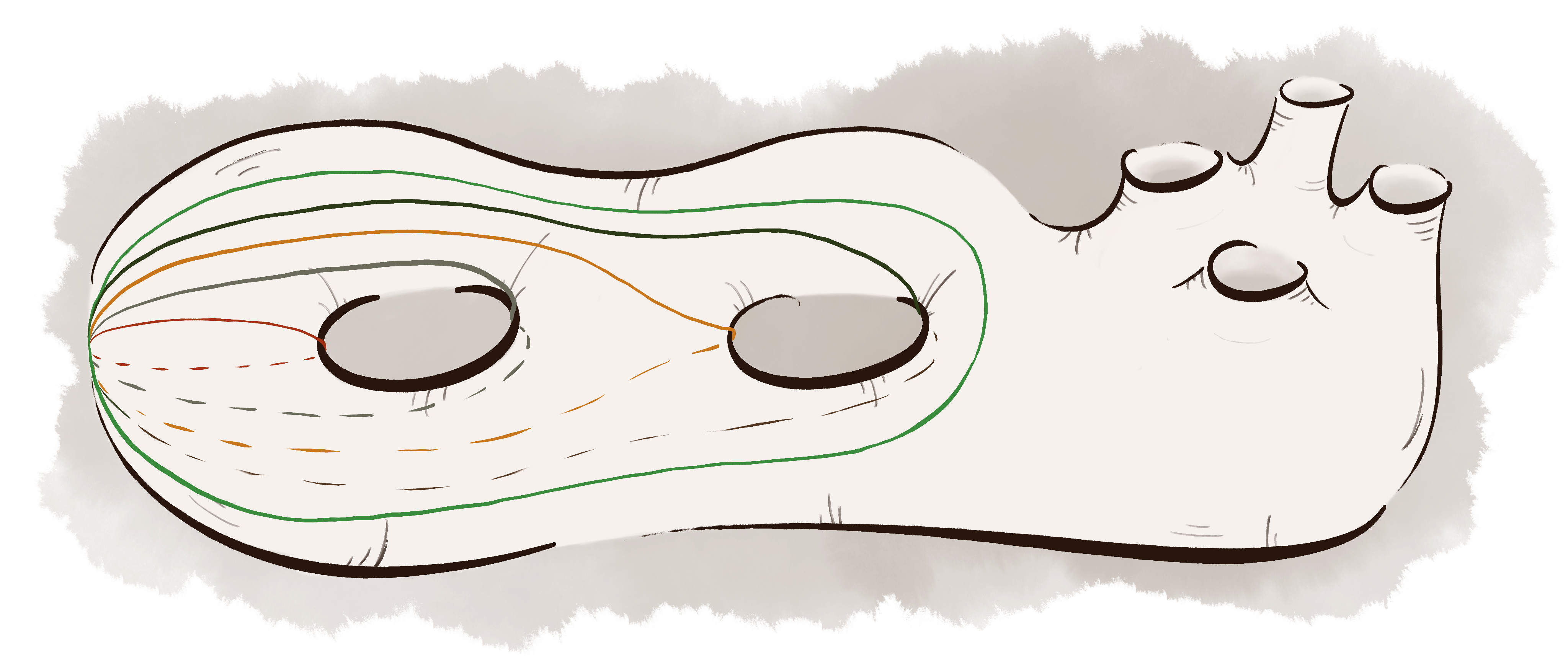
Systems of Curves on Non-Orientable Surfaces
Undergraduate Thesis: Gauss-Bonnet Theorem for Surfaces and Its Applications (in Chinese)
Talks
Linear Bound for Kakimizu Complex Diameter of Hyperbolic Knots
December 2025Linear Bound for Kakimizu Complex Diameter of Hyperbolic Knots
December 2025Geometric Intersection Complexes
January 2025Maximal Systems of Curves on Surfaces
October 2024Maximal Systems of Curves
September 2024Maximal Systems of Curves Intersecting Pairwise Once on Non-Orientable Surfaces
April 2024Maximal Systems of Intersecting Curves on Surfaces
December 2023Maximal Systems of Intersecting Curves on Surfaces
December 2023Seminars
G2T2 Seminar
Beijing
2025-
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Organizers:
Yifei CAI, Xiao CHEN, Diptaishik CHOUDHURY, Qiliang LUO, Tuo SUN, Ivan TELPUKHOVSKIY, and Daxun WANG
Latest Seminar:
Dec. 26, 2025, 15:00-16:30 PM
Place: Ningzhai 203
Speaker: Thiago de PAIVA (Peking University)
Title: Rigidity of Closed Braids over a Knotted Cabling Tori
Abstract:
In this talk we study the conjugacy problem for closed braids, which asks when two braids with the same number of strands, representing the same link, are isotopic through an isotopy that fixes the braid axis. This problem has numerous applications in braid theory and low-dimensional topology. We show that for closed positive braids arising from a generalized cabling over a fixed collection of knotted cabling tori, conjugacy of the companion braids carried by the torus cores forces conjugacy of the corresponding outer braid representatives. Equivalently, when the positive braid structure is supported on knotted cabling tori, the geometric cabling data rigidly determines the closed braid representation up to conjugacy. In particular, Markov stabilization is unnecessary. In the special case of positive braids containing a full twist, our results produce large families of satellite links whose minimal braid representatives are unique up to conjugacy. This extends classical rigidity results for iterated torus links to more general satellite constructions with unrestricted patterns. As an application, we obtain a partial verification of the Birman–Kofman conjecture for Lorenz links whose complements contain an essential torus given by the boundary of a tubular neighborhood of a torus link.
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Latest Seminar:
YMSC Topology Seminar
The YMSC Topology Seminar is devoted to frontier topics in topology, geometry, and related fields. It regularly invites scholars from across the mathematical community to share their work and engage in meaningful exchange, with the aim of fostering academic dialogue and broadening intellectual horizons.