About Me

My name is CHEN Xiao (陳 嘯). I received my Ph.D. in Mathematics from Tsinghua University, under the supervision of Prof. HUANG Yi (黃 意). My research interests include hyperbolic geometry, knot theory, combinatorial topology, and Teichmüller theory. Here is my Curriculum Vitae.
Beyond mathematics, I am also engaged in research on Chinese dialectology, with a particular focus on the Hangzhou dialect, a subvariety of Wu Chinese.
Email: x-chen20 [AT] tsinghua [DOT] org [DOT] cn
Research & Publications
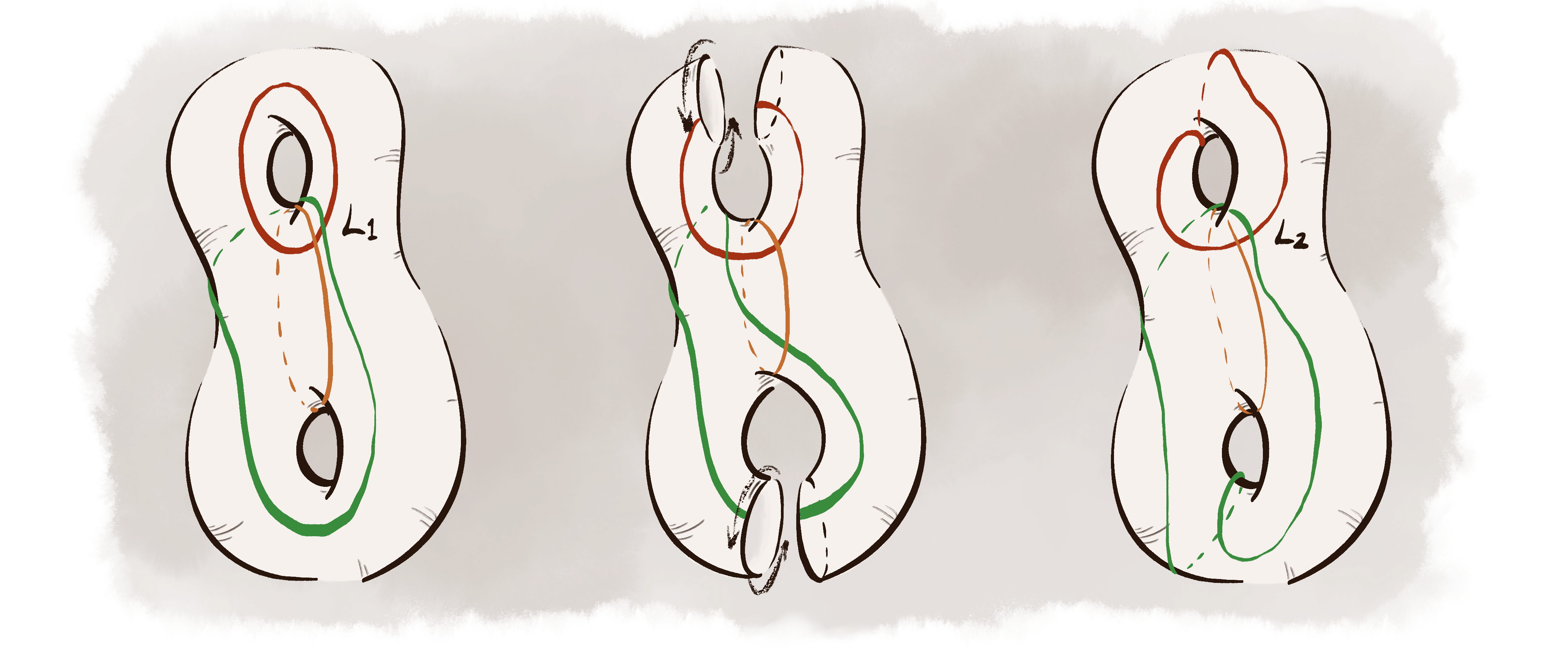
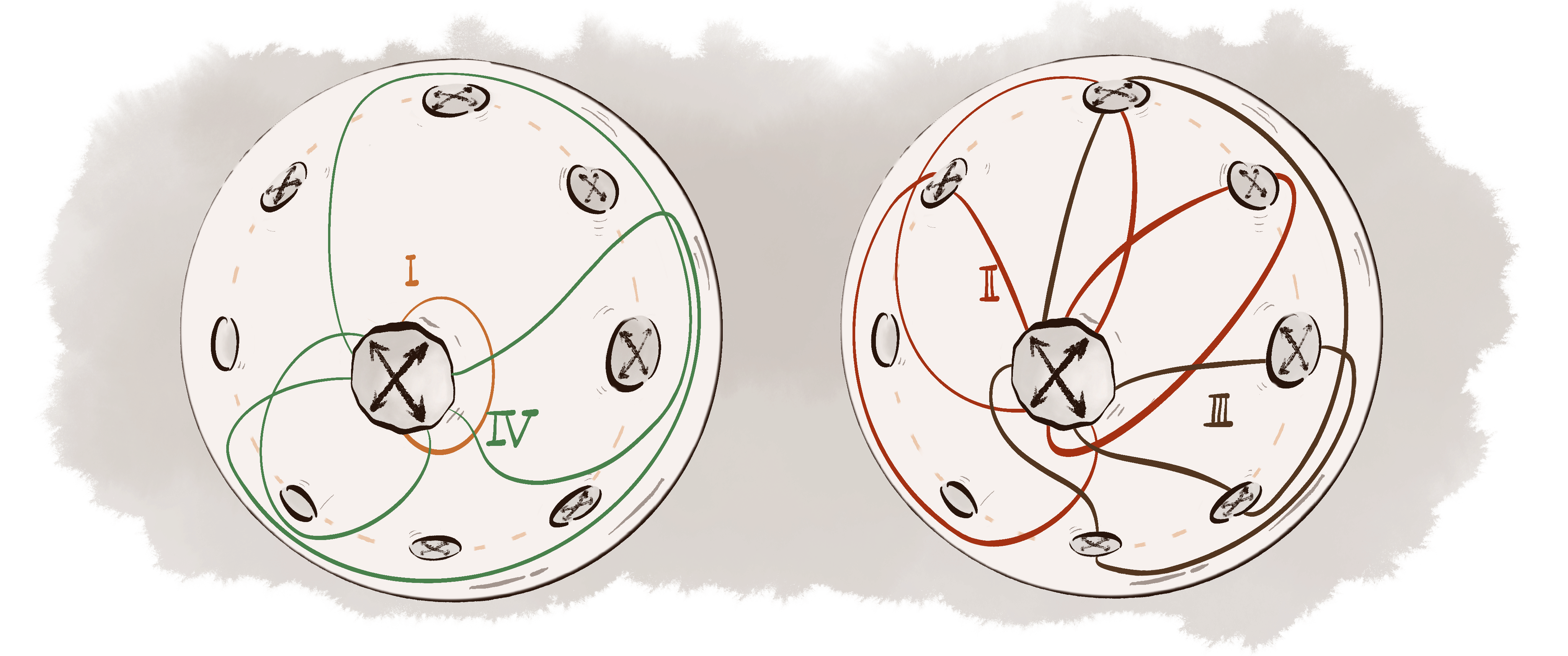
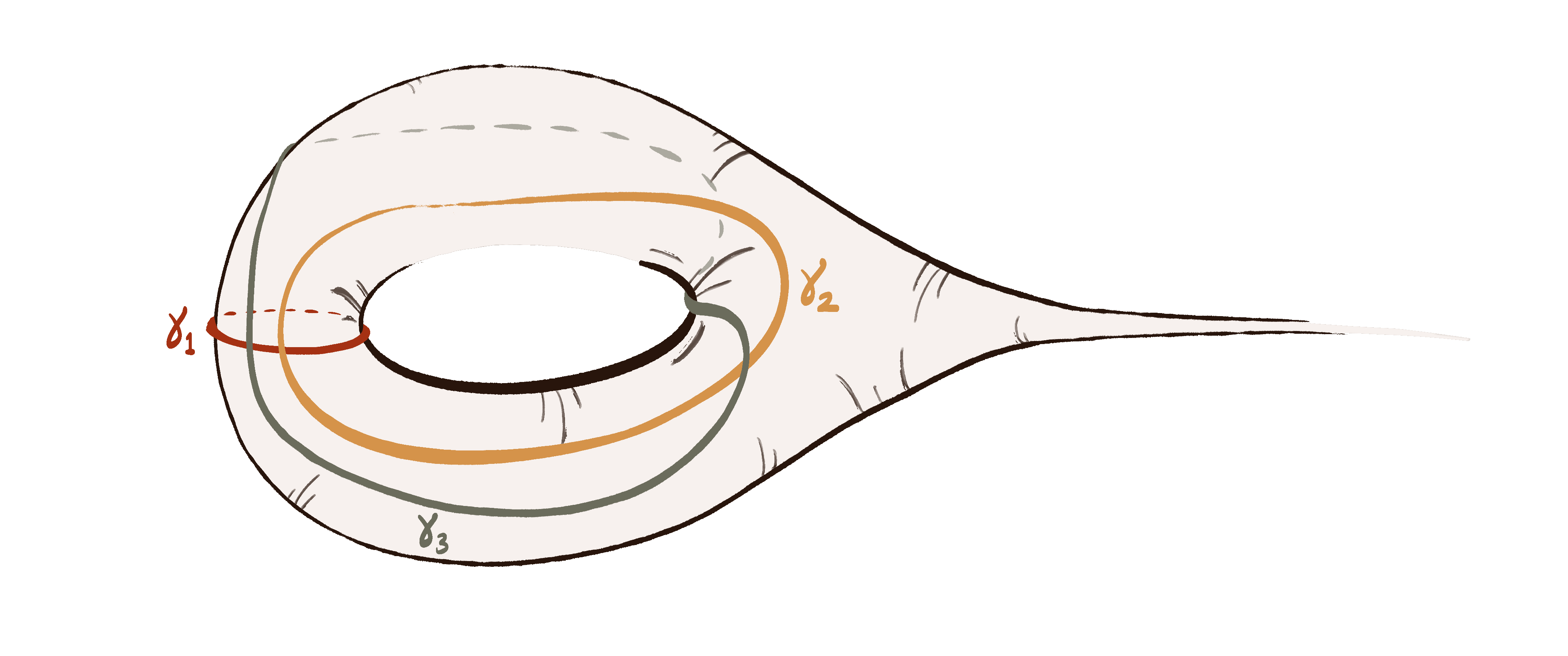
Linear Bound for Kakimizu Complex Diameter of Hyperbolic Knots (Joint with Wujie Shen)
Uniqueness of Maximal Curve Systems on Punctured Projective Planes (Joint with Wujie Shen)
Systems of Curves on Non-Orientable Surfaces
Undergraduate Thesis: Gauss-Bonnet Theorem for Surfaces and Its Applications (in Chinese)
Talks
Geometric Intersection Complexes
January 2025Maximal Systems of Curves on Surfaces
October 2024Maximal Systems of Curves
September 2024Maximal Systems of Curves Intersecting Pairwise Once on Non-Orientable Surfaces
April 2024Maximal Systems of Intersecting Curves on Surfaces
December 2023Maximal Systems of Intersecting Curves on Surfaces
December 2023Seminars
G2T2 Seminar
Beijing
2025-
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Organizers:
Yifei CAI, Xiao CHEN, Diptaishik CHOUDHURY, Qiliang LUO, Tuo SUN, Ivan TELPUKHOVSKIY, and Daxun WANG
Latest Seminar:
Time: Oct. 31, 2025, 10:00 AM
Place: Ningzhai 203
Speaker: Yujie LIN (Tsinghua University)
Title: The Boundary Dehn Twists on Punctured K3 Surfaces
Abstract:
In 4-manifold topology, Dehn twists along Seifert fibered 3-manifolds provide an important source fof exotic diffeomorphisms. A notable example is the boundary Dehn twist on a punctured K3 surface, which Baraglia-Konno and Kronheimer-Mrowka proved is nontrivial in the smooth mapping class group relative to boundary. I will show that despite being smoothly nontrivial, this diffeomorphism is trivial in the abelianization of the mapping class group. The proof is based on an obstruction for Spin^\mathbb{C} families due to Baraglia-Konno and the global Torelli theorem of K3 surfaces.
The G2T2 Seminar is organized by Ph.D. students and postdoctoral researchers at Tsinghua University specializing in geometry and topology, serving as an academic platform for exchange. The name “G2T2” refers to the three major fields of Geometry, Group Theory, and Topology, as well as their interdisciplinary directions. The seminar aims to foster mutual encouragement among young scholars, stimulate academic thinking, and broaden research horizons.
Latest Seminar:
YMSC Topology Seminar
The YMSC Topology Seminar is devoted to frontier topics in topology, geometry, and related fields. It regularly invites scholars from across the mathematical community to share their work and engage in meaningful exchange, with the aim of fostering academic dialogue and broadening intellectual horizons.